Have you ever been waiting in line for something and said to yourself, “I wonder what kind of data structure this is?”

No? Me neither. But data structures are fundamental to providing order in our lives, and they’re everywhere. They are also fundamental to computer science and algorithm design, which makes having a strong understanding of data structures critical to landing a software engineering job.

Queues

A queue is a useful data structure used in software engineering and other disciplines, and it has special properties that make it particularly important in those fields. Queues adhere to the First In First Out (FIFO) rule, where the item that has been in the queue the longest will be the next item removed.

Much like people on a ski lift, taking the escalator, or in a line of almost any kind, the queue appears all over the place in the real world. Your order is determined by virtue of where you are in the queue relative to the other people in the queue. If there is no one in front of you, then you are at the front of the queue.

The benefit of this data structure used in this setting is that there is no need for any additional mechanism; there isn’t any extra overhead needed to maintain order. Because of this, a downside to this data structure is that you must remain in the queue the entire time. Other variants of this data structure alleviate this problem, like a ticketing system at a butcher shop or waiting for your number to be called at the DMV. These variants still use a queuing system, but you don’t need to remain physically in line because you are assigned a number and the numbers remain in the queue in place of you.

Efficiency

When working with data structures, efficiency is critically important. Using the wrong data structure could result in an inefficient application and a poor user experience. So it is important to choose the correct data structure for your algorithm and efficiency is the metric we use to make these decisions. We generally use Big O notation to describe both time and space complexity, and you can see a comparison of popular data structures here in this cheatsheet.

We’re often primarily interested in the time complexity of a data structure when comparing them because space complexity for data structures in isolation is almost always linear (i.e. O(n)). We’re also usually interested in the worst-case scenarios when evaluating time complexity. This is because, for small amounts of data, the time complexity is often trivial and unreliable.

Queues, when used properly, are well-suited for insertion and deletion. This is due to there only being one location you can insert an item (at the back of the queue) and only one location from which you may delete an item (at the front of the queue). Due to these constraints, queues have a time complexity for insertion of O(1), or “constant” time complexity. However, if you need to be able to look up any other item other than the one at the front of the queue, you’re out of luck. You would need to dequeue each item until you reached your target item, which would often be untenable. In that case, your time complexity would be O(n), and you may want to consider a different data structure to suit your needs.

Implementation in JavaScript

At the very minimum, a queue needs to be able to enqueue an item and dequeue the longest-tenured item, as well as allow users to read its length. Below is a functional implementation of a basic queue in JavaScript.

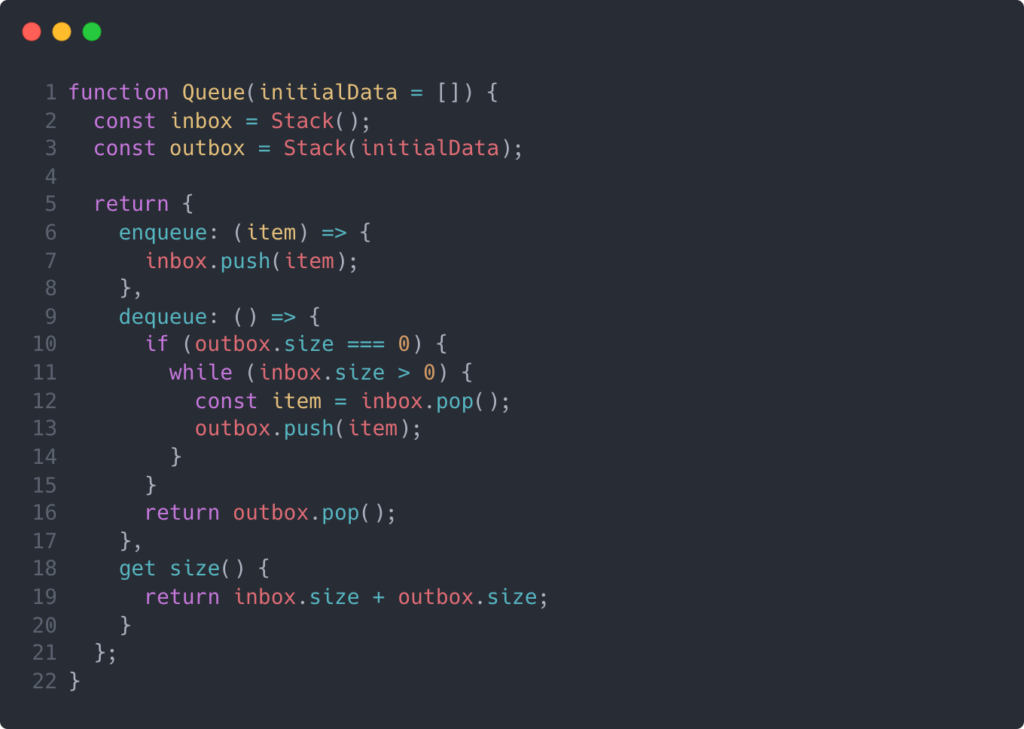
First, you might notice that I chose to implement this queue using a function instead of a class. This is because I wanted to keep my inbox and outbox private, and I used JavaScript closures to achieve this. If I were to have implemented this using a class, I would have placed the inbox and outbox onto the class instance which would have exposed them to the outside scope.

Second, you may have also noticed that I’m invoking a Stack function. This is a custom implementation of a stack in JavaScript, and if you’d like to see how I built it, please read my previous article How to Build a Stack in JavaScript where I walk through all the details behind the stack implementation. Stacks use the Last In First Out (LIFO) principle and are optimized to provide constant time complexity (i.e. O(1)) for insertions and deletions.

Stacks come into play here because of efficiency. A simple implementation of a queue might just involve an array where you enqueue items by inserting them into the array at index 0 and shifting the rest of the items over by 1 index. The “shifting” in the array is expensive and would make your insertion time complexity linear, or O(n).

To get around this limitation, we can implement two stacks: an inbox and an outbox. When items are enqueued onto the queue, we push them onto the inbox stack. That operation is constant time complexity. Every time we need to dequeue an item, we first check if there are any items in the outbox. If there’s at least one item, we simply pop it off of the stack and return that item, which is constant time complexity. In the case where our outbox is empty but our inbox has items, we pop off each item in the inbox and push it onto the outbox stack. This operation is considered “amortized” constant time complexity. We use the term “amortized” to describe operations that are occasionally worse than what their typical time complexity would indicate. In our case, we have constant time dequeues until we run out of items in our outbox. Then we have an O(n) operation to move all of the items from the inbox to the outbox. Because this only happens periodically and not on every dequeue request, we can say that this operation is constant amortized time, or O(1)+. I’ve illustrated these operations below for clarity.

Once you understand the mental model, the code is fairly trivial. We return an object that has an enqueue method, a dequeue method, and a size getter. Enqueue pushes the target item to the inbox. Dequeue checks if we have items in the outbox, and if we do, it will just pop off the latest item and return it. If we don’t, it’ll run through the logic I’ve illustrated above and then pop off the latest item (if any). And finally, the size getter just returns the sum of our stack sizes.

Conclusion

Queues are very common in our lives and are a fundamental data structure used in software engineering. They are designed to be efficient for data insertion and deletion when properly used. Hopefully, this article has helped to provide some clarity around queues.