Recursion is a programming technique where a function calls itself to solve a particular problem. It’s especially effective for problems that can be divided into smaller, similar subproblems. By breaking down a complex problem in this way, recursion can often lead to elegant and concise solutions.

A recursive function repeatedly calls itself with smaller versions of the problem until it reaches a simple, solvable base case. This self-referential approach is a powerful tool for tackling problems that have a recursive structure.

A Real-Life Analogy of Recursion

While the concept can be challenging to grasp, recursion can be likened to solving a jigsaw puzzle. Some puzzle solvers might start by connecting a few pieces together that have similar colors, and they might do so until they have a few groupings of puzzle pieces. They might then connect those groupings into one larger grouping. This strategy can go on until the entire puzzle is completed.

Recursion Fundamentals

For some, it can be easier to learn by reading code, but before we can demonstrate recursion by programming out an example, we need to explain some fundamental concepts of recursion.

In recursion, “cases” are the different scenarios that dictate how a recursive function behaves. These cases logically guide the function on whether to continue recursing or to terminate. Correctly identifying and implementing these cases is essential to ensuring that a recursive function works as intended and doesn’t fall into an infinite loop.

There are typically two primary cases in recursion: the base case and the recursive case.

Base Case

The base case is the condition under which the recursive function stops calling itself. It is the simplest instance of the problem that can be solved directly without further recursion, and it is critical because it prevents infinite recursion by providing a stopping point. The base case stops the recursion when the problem has been reduced to its simplest form or has reached the end of the sequence.

Recursive Case

The recursive case is the condition under which the function continues to call itself with modified arguments. In these scenarios, the function makes progress towards the base case by simplifying or reducing the problem with each recursive call. The recursive case helps to break the problem into smaller sub-problems that have the same structure as the original problem, but with simpler or reduced inputs.

Recursion in JavaScript

Let’s recreate the Math.pow method, which calculates the power of a number, using recursion in JavaScript. The Math.pow(base, exponent) function computes the result of raising thebase value to the power of an exponent.

Recursive Math.pow Implementation

To implement this method using recursion, we’ll use two main cases:

1. Base Case: If the exponent is 0, the result is 1 because any number raised to the power of 0 is 1.
2. Recursive Case: Multiply the base by the result of the function with the exponent decremented by 1.

Here’s the JavaScript implementation:

function recursivePow(base, exponent) {
  if (exponent === 0) {
    return 1;
  } else if (exponent < 0) {
    return 1 / recursivePow(base, -exponent);
  } else {
    return base * recursivePow(base, exponent - 1);
  }
}

Explanation of the Code

1. Base Case: If the exponent is 0, the function returns 1. This stops the recursion from continuing indefinitely.
2. Edge Case: If the exponent is negative, the function inverts the base (i.e. calculates 1 / base) and calls itself with the positive value of the exponent. This allows the function to correctly compute the result for negative exponents.
3. Recursive Case: If the exponent is positive and greater than 0, the function multiplies the base by the result of calling itself with the exponent decremented by 1. The decrementing by one is critical because this causes the recursive calls to home in on base case (i.e. reducing the exponent by 1 until it reaches 0).

How the Recursion Unfolds

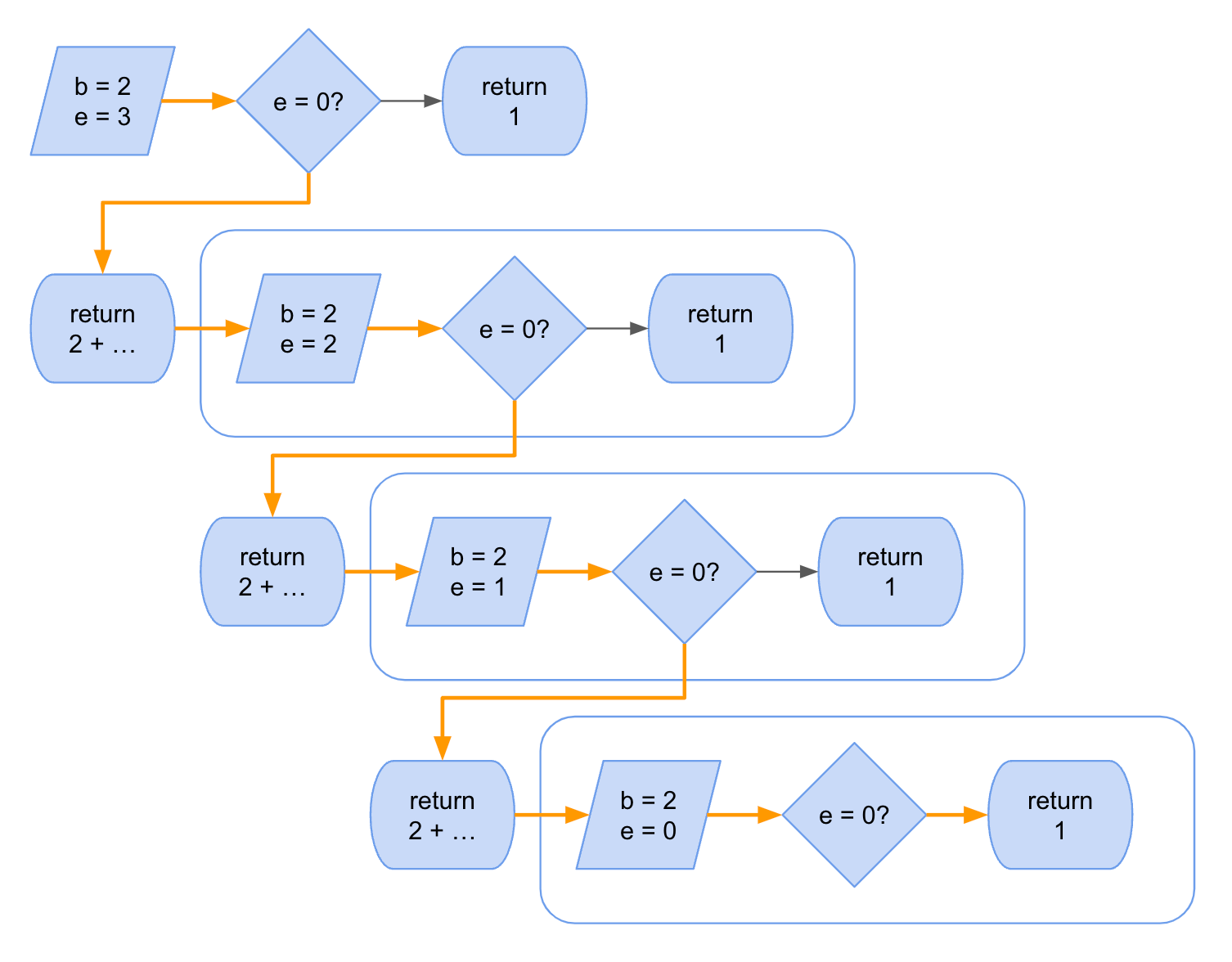
Let’s walk through an example where we invoke the recursive power function with a base of 2 and a power of 3 (recursivePow(2, 3)). Note, in the illustration above, I’ve omitted the edge case logic for visual clarity.

1. recursivePow(2, 3) returns 2 * recursivePow(2, 2)
2. recursivePow(2, 2) returns 2 * recursivePow(2, 1)
3. recursivePow(2, 1) returns 2 * recursivePow(2, 0)
4. recursivePow(2, 0) returns 1 (base case)
5. As the call stack unwinds and the function invocations return their values, the result is equivalent to: 2 * 2 * 2 * 1 = 8.

This implementation of Math.pow using recursion is a great way to illustrate the power of recursion by breaking down problems into smaller sub-problems, solving them recursively, and combining the results to obtain the final solution.

The Pros and Cons of Using Recursion

Pros of Using Recursion

• Optimal Technique: For problems that involve manipulating or iterating through dynamic data structures—such as traversing through a tree or linked list—or while designing solutions that involve sorting or using a divide-and-conquer strategy, recursion naturally lends itself to elegant implementations in these scenarios.
• Brevity: Recursion can often require fewer lines of code compared to their equivalent iterative solutions, which can make the codebase less verbose and cleaner.

Cons of Using Recursion

• Performance Overhead: Recursion can be less memory-efficient than iterative solutions due to the overhead of multiple function calls. Each recursive call adds a new frame to the call stack, which can lead to excessive memory usage and a higher space complexity.
• Risk of Stack Overflow: Anyone first learning about recursion has probably caused a stack overflow. If the recursion depth becomes too deep, it can lead to a stack overflow error, especially in languages with limited stack size. This happens when there are too many nested function calls before reaching the base case. While tail call optimization —where the recursive case is in the tail position and therefore could optimized to not grow the call stack—few JavaScript engines have implemented support for this ECMAScript 6 feature.
• Debugging Difficulty: Recursive functions can be harder to debug and trace, especially if the base case is not correctly defined, leading to infinite recursion.

When to Use Recursion

Recursion is particularly useful when dealing with problems that have a natural recursive structure, such as:

• Tree Traversal: Traversing hierarchical data structures like binary trees or graphs is more intuitive with recursion.
• Divide and Conquer Algorithms: Algorithms like QuickSort and MergeSort benefit from recursion as they divide the problem into smaller subproblems.
• Dynamic Programming: Some dynamic programming problems, such as calculating Fibonacci numbers, can be solved using recursion (though they may require memoization to optimize performance).

Conclusion

Recursion is a powerful tool in a programmer’s toolkit that allows for elegant and concise solutions to complex problems. However, it’s essential to understand when and how to use recursion effectively, considering both its advantages and potential pitfalls. By carefully structuring recursive functions and being mindful of base cases and stack depth, you can harness the full potential of recursion in your software projects.

---

If you enjoyed this article, check out How to Build a Hash Table in JavaScript.